5.12 Atomi (diskreetit energiatasot, siirtymät ja tilastolliset rajoitteet)

Etusivu ／ Luku 5: Mikroskooppiset hiukkaset

I. Laajuus ja tavoitteet

Tässä osassa selitämme kolme ydinasiaa selkeällä yleiskielellä:

• Diskreetit energiatasot: miksi atomin elektroni “viipyy” vain harvoissa sallituissa kuorissa ja muodoissa eikä millä tahansa energialla.
• Siirtymät ja spektrit: miten elektroni vaihtaa kuorta, miten se “kuittaa” energiaeron valona ja miksi spektriviivat ovat diskreettejä ja erivoimaisia.
• Tilastolliset rajoitteet: mitä tarkoittavat “yksittäis-” ja “parisijoitus”, miksi “kahta hiukkasta ei sallita täsmälleen samaan tilaan”, miten Hundin sääntö toimii ja millaisen aineellisen kuvan energiafilamenttiteoria (EFT) tarjoaa.

Kirjoitustapa: ei raskaita kaavoja; tarvittaessa arjen analogioita (esimerkiksi “luokkahuone ja istumapaikat”, “todennäköisyyspilvi”). Symbolit n, l, m, ΔE ja Δl toimivat vain tunnisteina.

II. Oppikirjakooste (vertailuperusta)

• Ydin tuottaa Coulombin potentiaalin; elektronit asuttavat kvanttitiloja, jotka täyttävät reuna- ja symmetriaehdot.
• Sallitut tilat merkitään pääkvanttiluvulla n, rataliikemäärän kvanttiluvulla l, magneettisella kvanttiluvulla m ja spinillä; s/p/d/f vastaavat l = 0/1/2/3.
• Samaan atomiin kuuluvat elektronit noudattavat Fermin–Diracin tilastoa ja Paulin kieltoperiaatetta: yhteen kvanttitilaan mahtuu enintään kaksi vastakkaisspinistä elektronia.
• Siirtymät tottelevat valintasääntöjä (tyypillisesti Δl = ±1); energiaero ΔE tasataan fotoneina, jolloin syntyy diskreettejä viivoja; viivan voimakkuus määräytyy siirtymän matriisialkion perusteella; viivanleveyteen vaikuttavat luonnollinen leveytyminen, Doppler, törmäykset ja ulkoiset kentät.

Tämän koetellun empiiris-teoreettisen rungon päälle energiafilamenttiteoria rakentaa yhtenäisen, aineellisen ja intuitiivisen näkymän.

III. Energiafilamenttiteorian ydin: matala tensorikaukalo + seisovan vaiheen kanavat filamenttirenkaalle

1. Energiameri: tyhjiö nähdään “merenä”, jolla on väliaineen piirteitä; sen säädettävää “kireyttä” kutsutaan tensoriksi. Tensor asettaa paikalliset asteikot “etenemisrajalle”, vaimennukselle ja ohjaukselle.
2. Matala tensorikaukalo: atomin ydin “painaa” energiameereen lähes isotrooppisen matalan kaukalon. Kaukana se näyttäytyy massana ja ohjauksena; läheltä se rajaa elektronin pysyvien tilojen geometrian.
3. Elektroni suljettuna filamenttirenkaana: elektroni ei ole piste, vaan itseään ylläpitävä suljettu energiafilamentti. Jotta se “pysyisi hajoamatta”, renkaan on lukittava vaiherytminsä seisovan vaiheen kanaviin, jotka ympäröivä tensorimaasto kaivertaa.
4. Seisovan vaiheen kanava = sallittu energia + sallittu muoto:
   • s-kanava: pallosymmetrinen “vyö-/rengasmaisen” pilven hahmo.
   • p-kanava: kolme keskenään kohtisuoraa “käsipainopilveä”.
   • d/f-kanavat: suunnattuja ja monimutkaisempia geometrioita.
5. Intuitio: diskreetit tasot ovat ne harvat kanavat, joissa rengas voi sulkea vaiheen ja minimoida energian matalassa kaukalossa. Kanavia on vähän, siksi spektri on diskreetti.

IV. Miksi tasot ovat diskreettejä (EFT-intuitio)

• Reuna + säästeliäisyys: pysyäkseen koossa rengas tasapainottaa sisäisen rytminsä kaukalon “takavedon” kanssa, jolloin syntyy vakaa silmukka. Vain harvat geometrian ja rytmin yhdistelmät yltävät samanaikaisesti “suljettu ja säästäväinen” — nämä ovat diskreetit paikat n, l, m.
• Muoto valikoituu maastosta: lähes pallomainen kaukalo suosii ensin s-muotoa; kun kulmaliikemäärää on kannettava, geometria “kasvaa” kaksiliuskaiseen p-muotoon ja siitä ylöspäin d/f-muotoihin. Muoto ei ole pelkkä etiketti vaan kompromissi maaston, vaiheen ja energiakulun välillä.
• Hierarkia: ulommat kanavat ovat väljempiä ja heikommin sidottuja, mutta herkempiä särkyville häiriöille — siksi korkeat viritykset (suuri n) ionisoituvat helposti.

V. Tilastolliset rajoitteet: yksittäis-, pari- ja “ei kaksoissijoitusta samaan tilaan”

1. Kieltoperiaate aineellisena (Pauli):
   Jos kaksi rengasta kulkee samassa kanavassa samassa vaiheessa, lähikenttään syntyy tensorin leikkausristiriitoja; energiakustannus karkaa ja rakenne menettää kantonsa. Kaksi reittiä:
   • Siirtyä toiseen kanavaan (vastaa “ensin yksittäissijoitus”).
   • Parittua vaihekomplementaarisesti samassa kanavassa (vastaa “vastakkaiset spinit”), jolloin kaksi elektronia voi jakaa saman pilven ilman tuhoisaa leikkausta — tämä on parisijoitus.
2. Kolme tilannetta:
   • Tyhjä: kanavassa ei ole rengasta.
   • Yksittäinen: yksi rengas yksin — usein vakain.
   • Pari: kaksi vaihekomplementaarista rengasta yhdessä — vakaa, mutta hieman energiaa kuluttavampi kuin kaksi erillistä yksittäistä.
3. Hundin sääntö aineellisesti:
   Kolminkertaisesti degeneroituneessa joukossa (pₓ/pᵧ/p𝓏) renkaat levittäytyvät ensin yksittäisinä eri suuntiin jakamaan lähikentän leikkausta ja minimoimaan kokonaisenergian. Vasta pakon edessä muodostuu pari yhteen suuntaan. Näin abstrakti “kapasiteetti kaksi; yksittäinen ennen paria” juurtuu tensorin leikkauskynnyksiin ja vaiheen komplementaarisuuteen.

VI. Siirtymät: miten elektroni “kuittaa” valona

1. Käynniste: ulkoinen syöttö (kuumennus, törmäykset, optinen pumppaus) tai sisäinen uudelleenjako nostaa renkaan matalasta kanavasta korkeaan; korkea tila on lyhytikäinen ja palaa viiveen jälkeen säästäväisempään kanavaan.
2. Minne energia menee: kanavan vaihtaminen synnyttää ylijäämää tai vajetta, joka poistuu/tulee sisään häiriöpaketteina energiameressä — makrotasolla valona.
   • Emissio: korkea → matala, paketti ulos (emissioviiva).
   • Absorptio: matala → korkea, paketti sisään kanavaeron mukaisena (absorptioviiva).
3. Miksi viivat ovat diskreettejä: kanavat ovat diskreettejä, joten ΔE voi olla vain nuo “kanavaerot”, ja fotonien taajuudet asettuvat muutamiin arvoihin.
4. Valintasäännöt intuitiivisesti: siirto vaatii muodon ja käteisyyden (chiraliteetin) sopivuuden, jotta kulmaliikemäärä ja suunta tasapainottuvat energiaveden kanssa:
   • Δl = ±1 on luettavissa “yksi askel muodonvaihtoa”, joka tasaa energia–kulmaliike–kytkentätehokkuuden.
   • Δm-kuvio syntyy kytkennän geometriasta ulkoisten orientaatiodomeenien (kentät, polarisaatio) kanssa.
5. Viivan voimakkuus: määräytyy yhdessä “vaihepeittoalan” ja “kytkentäesteen” mukaan: suuri peitto ja pieni este → voimakas oskillaattori, kirkas viiva; pieni peitto ja suuri este → kielletty/ heikko siirtymä, himmeä viiva.

VII. Viivaprofiili ja ympäristö: miksi sama viiva voi leveneä, siirtyä tai halkaistua

• Luonnollinen leveys: virittyneiden tilojen rajallinen elinaika antaa kanavalle oman “ikkunan” — luonnollisen levenemisen.
• Lämpöliike (Doppler): koko atomin liike siirtää taajuuksia hienoisesti ja summautuu gaussimaiseen leventymään.
• Törmäykset (paineleventyminen): toistuva “puristus–löysäys” naapurustosta heiluttaa vaihetta ja leventää viivaa.
• Ulkoiset kentät (Stark/Zeeman): orientaatiodomeenit muokkaavat kanavan “reunageometriaa”, poistavat degeneraatiota ja tuottavat ennustettavia halkemisia ja siirtymiä.
• EFT yhdellä virkkeellä: viivaprofiili = kanavan oma ikkuna + “värinä–uuskalointi–halkaisu”, kun kanava on upoksissa ympäristön tensorissa ja orientaatiodomeeneissa.

VIII. Miksi “suurempi ympäristön tensori → hitaampi sisäinen rytmi → matalampi emissio­taajuus”

“Suurempi ympäristön tensori” tarkoittaa, että matalan kaukalon laajempi konteksti (voimakkaampi gravitaatiopotentiaali, suurempi puristus/tiheys, vahvat orientaatiodomeenit) kiristää energiavettä. Erotamme kaksi suuretta:

• Etenemisraja: nopein vaste, jota väliaine tukee.
• Seisovan vaiheen taajuus: ympäristökuorman alla olevan sidotun moodin rytmi.

Ne eivät ole sama asia. Etenemisraja voi nousta, kun taas sidottu moodi hidastuu, koska ympäristö “vetää mukana”. Energiafilamenttiteoria yhdistää kolme vaikutusta:

1. Syvempi ja leveämpi kaukalo → pidempi silmukka (geometrinen viive): isofaasipinnat siirtyvät ulommas; samassa kanavassa jokainen kierros kulkee pidemmän suljetun reitin.
2. Enemmän välainetta kytkeytyy mukaan → suurempi efektiivinen hitaus (reaktiivinen kuorma): tiukempi lähikenttäkytkentä pakottaa jokaista vaihekiertoa “vetämään” paksumpaa välainetta; lisä“massa/reaktiivinen kuorma” hidastaa luontaista rytmiä.
3. Kaiku­takaisinkytkentä → vaihe-etenemä (ei-lokaali viive): häiriöt kaikuvat kaukalossa ja syöttävät takaisinkytkentää runkoon; jokainen kierros kerää “kaikuvaihetta”, ja reaktiivista energiaa on varastoida–luovuttaa enemmän → rytmi hidastuu.

Nettotulos: sidottujen moodien taajuudet laskevat; tasovälit kapenevat (usein lähes verrannollisesti); ΔE pienenee, joten emissio/absorptio siirtyy matalampiin taajuuksiin (punaisempaan).

Usein kysyttyä:

• “Eikö suurempi tensori nopeuta etenemistä?” — Vapaalle etenemisrajalle kyllä. Sidotut mallit ovat kuitenkin ympäristökuormattuja oskillaattoreita, joissa geometria + lisämassa + kaikoviive dominoivat ja hidastavat.
• “Onko tämä vain gravitaatiopunasiirtymä?” — Energiafilamenttiteorian kielellä vahvempi potentiaali ≡ suurempi tensori; atomin “paikallinen kello” hidastuu edellä kuvatuista kolmesta syystä. Havaittu punasiirtymä on yleisen suhteellisuusteorian mukainen — ja tässä sille annetaan aineellinen reitti väliainekytkennän ja geometrian kautta.

Havaittavia vihjeitä (intuitiivinen taso):

• Sama ydin, eri ympäristö: valkoinen kääpiö -tähtien lähellä mitatut viivat ovat punaisempia kuin laboratoriossa; laboratoriossa Starkin/Zeemanin/paineen poistamisen jälkeen jää tasainen punasiirtymä, joka kasvaa paineen/tiheyden/orientaation mukana.
• Isotoopit/analogiset järjestelmät: helpommin polarisoituvat (pehmeämpi lähikenttä) järjestelmät osoittavat voimakkaamman keskitaajuuden alenemisen samalla ympäristön tensorilla.

IX. Miksi elektroni näyttää pilveltä ja “harhailee sattumanvaraisesti”

Energiafilamenttiteoriassa elektroni on suljettu filamenttirengas, joka säilyy pitkään vain harvoissa seisovan vaiheen kanavissa, jotka ytimen tensorikaukalo kaivertaa. Näkyvä “pilvi” on renkaan esiintymistodennäköisyyden jakauma sallitussa kanavassa. Jos elektroni pakotetaan hyvin kapeaan sijaintivyöhykkeeseen, lähikentässä syntyy tensorin leikkausristiriitoja ja samalla liikemäärän (suunnan ja suuruuden) on levittäydyttävä silmukan sulkemiseksi — hinta on korkea. Siksi vakaa ratkaisu on rajallisen levyinen, mikä on “epävarmuuden” aineellinen juuri.

Energiameressä on tensorin taustakohina (TBN), joka antaa renkaan vaihe-rytmiin hienovaraisia ja jatkuvia tönäisyjä ja synnyttää hienojakoisia vaiheaskelia kanavan sisällä. Kanavan reunan ulkopuolella vaihe ei enää sulkeudu; tuhoisa itseinterferenssi vaimentaa amplitudia ja jättää tutun “tiheä–harva” -kuvion. Mittaus lokaloi elektronin hetkeksi (kiristää lähikenttää), minkä jälkeen järjestelmä palaa sallittuun seisovan vaiheen kuvioon. Tilastollisesti se näyttää pilveltä, joka “liikkuu” luvallisella alueella.

X. Yhteenvetona

• Diskreetit tasot: harvat seisovan vaiheen kanavat, joissa filamenttirengas sulkee vaiheen ja säästää energiaa ytimen tensorikaukalossa.
• Tilastolliset rajoitteet: kielto nousee kynnystä ylittävästä samavaiheisesta leikkauksesta; parisijoitus perustuu vaiheen komplementaarisuuteen; Hundin “yksittäinen ennen paria” minimoi kokonaisleikkauksen.
• Siirtymät ja spektrit: kanavan vaihto kuittaa energian häiriöpaketteina → diskreetit viivat; voimakkuus riippuu pilvien päällekkäisyydestä ja kytkentäesteestä.
• Ympäristö → hitaampi rytmi → matalampi taajuus: pidempi/syvempi silmukka (geometrinen viive) + lisähitaus (reaktiivinen kuorma) + kaikuetenemä (ei-lokaali) yhdessä laskevat sidottujen moodien taajuuksia ja kaventavat tasovälejä; tuloksena punasiirtymä, joka sopii gravitaatiohavaintoihin ja saa konkreettisen aineellisen mekanismin.

XI. Neljä tyypillistä atomia (elektroneineen) — kaavio

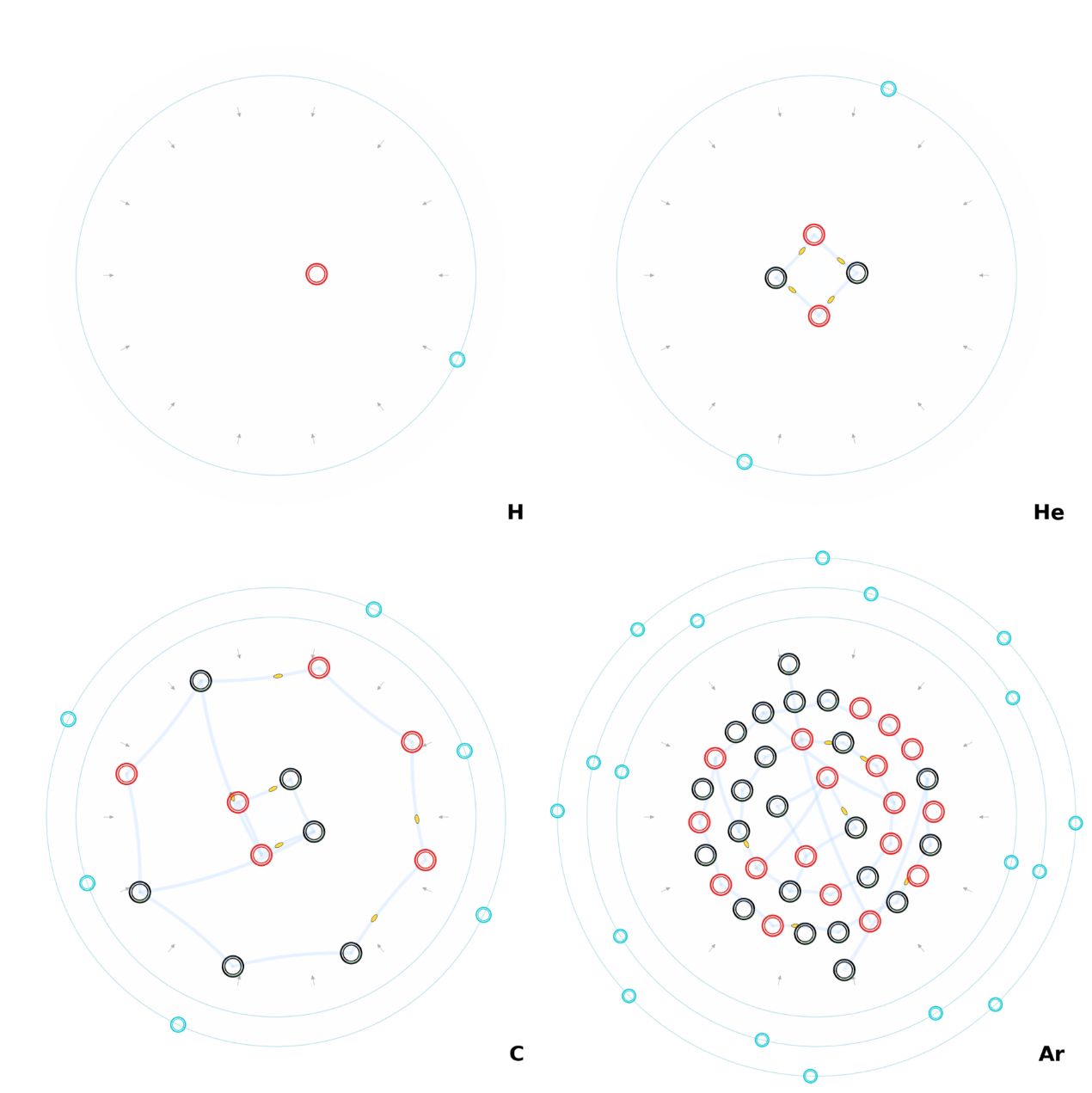
Selitteet (tyyli ja konventiot):

• Nukleonit: punaiset renkaat = protonit; mustat renkaat = neutronit.
• Värivuoputket: puoliläpinäkyvät siniset nauhat nukleonien välillä (nukleonien yli kulkevat tensorisidonnan kaistat); pienet keltaiset ellipsit kuvaavat gluonin ulkoasua.
• Elektronit: pienet syaanit renkaat diskreeteillä elektronikuorilla (vaaleansyaanit samankeskiset ympyrät).
• Oikea alakulma, valkoinen kenttä: alkuaineen symboli (esimerkiksi H, He, C, Ar).
• Isotoopit: H-1, He-4, C-12, Ar-40; kuoret havainnollistetaan ryhmittelyn [2, 8, 18, 32] mukaan (esimerkiksi Ar = [2, 8, 8]).